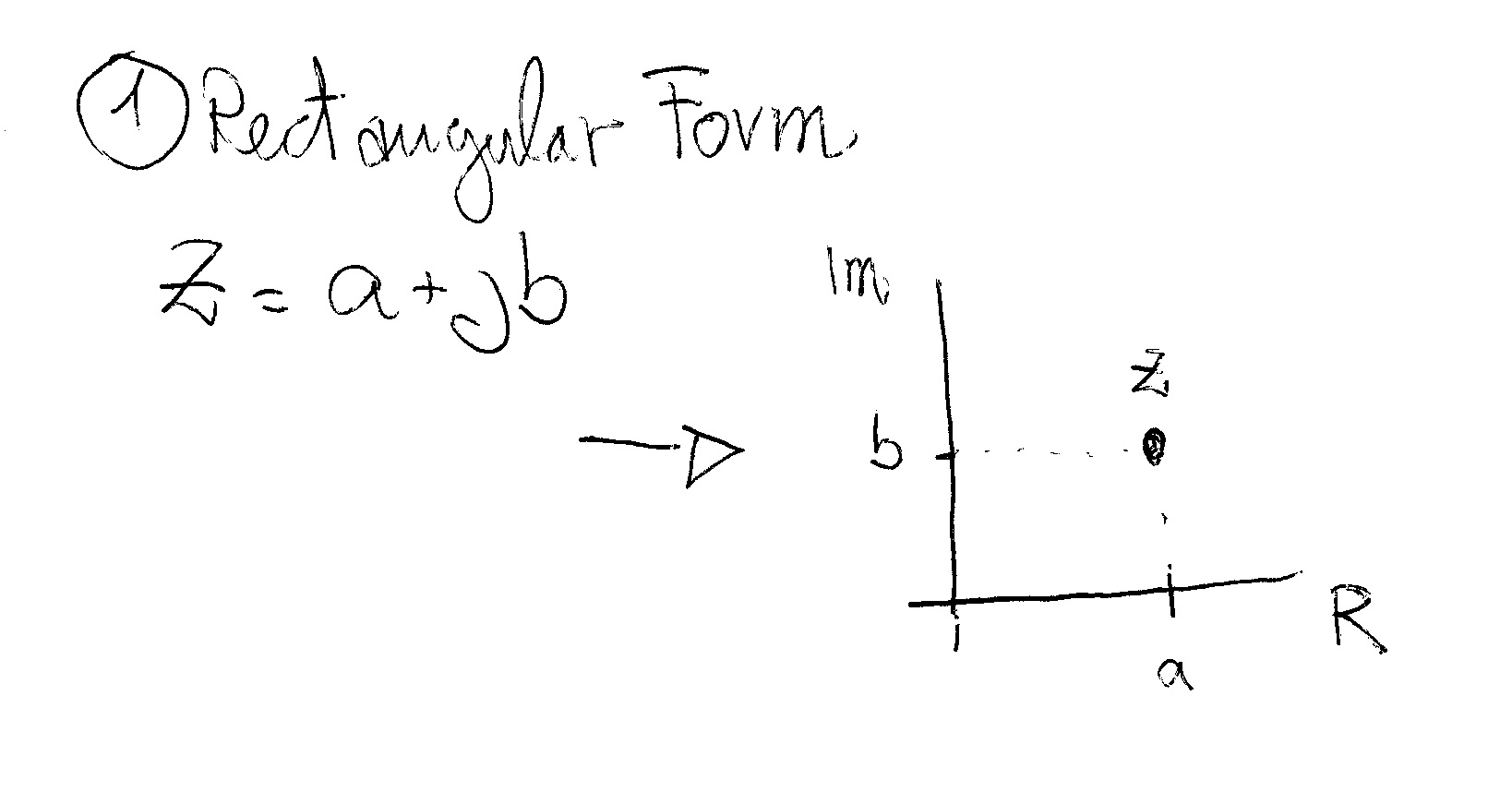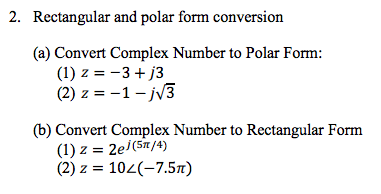Polar To Rectangular Form Complex Numbers

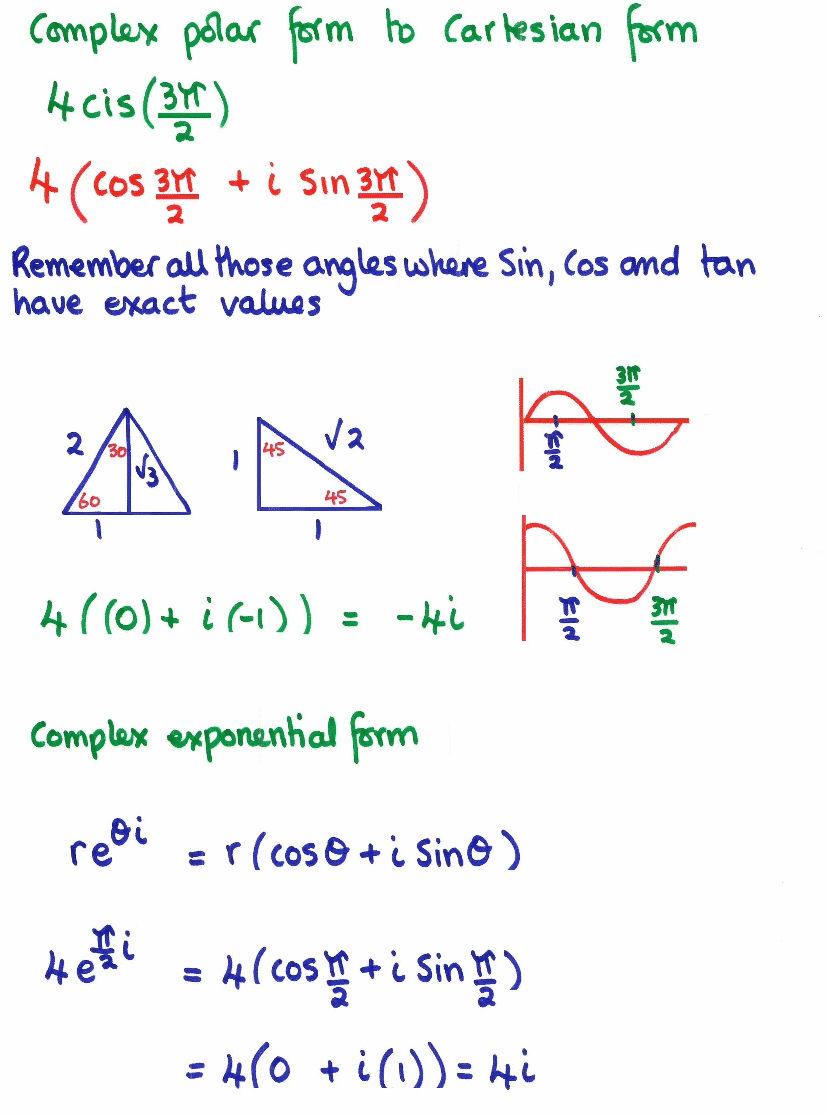
We first encountered complex numbers in precalculus i.

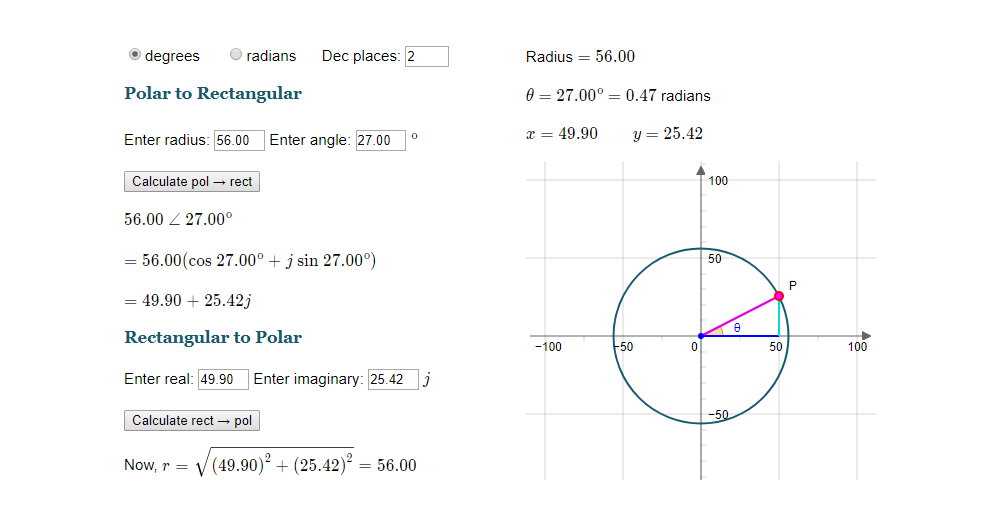
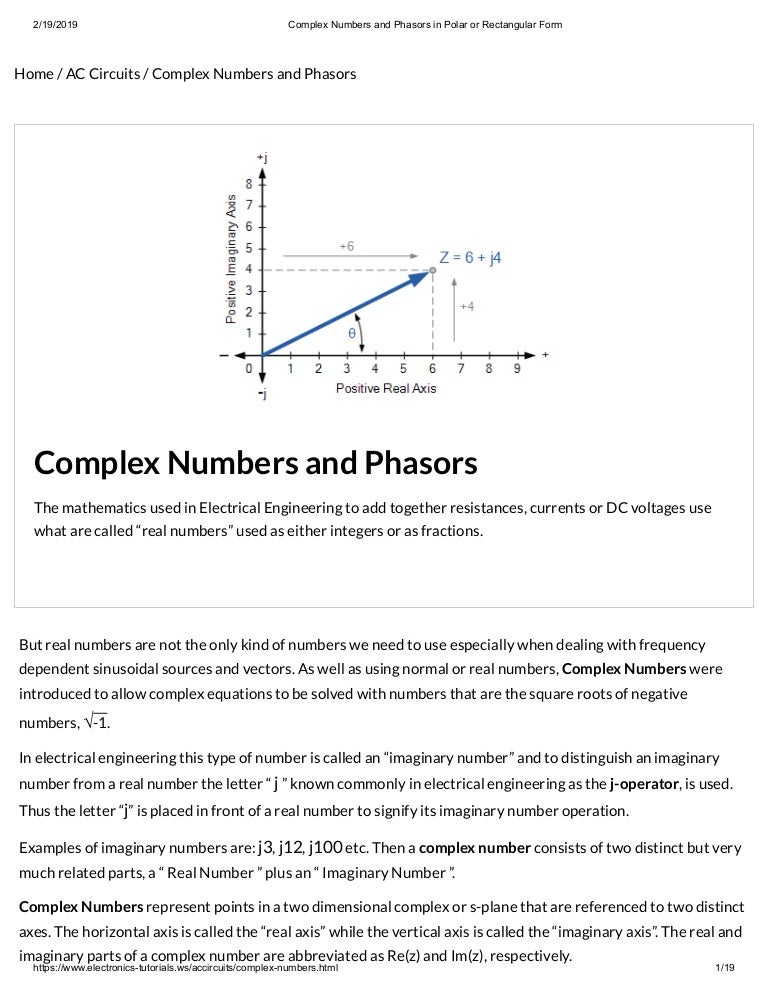
Polar to rectangular form complex numbers. To find the value of the complex number. Translation of complex numbers from polar form to rectangular form and vice versa interpretation of complex numbers in the scheme of applications and application of de moivre s theorem. We can think of complex numbers as vectors as in our earlier example. Complex numbers and polar form of a complex number interactive graph convert polar to rectangular and vice versa in the following graph the real axis is horizontal and the imaginary j sqrt 1 axis is vertical as usual.

The polar form of a complex number is another way to represent a complex number. In order to work with complex numbers without drawing vectors we first need some kind of standard mathematical notation there are two basic forms of complex number notation. But there is also a third method for representing a complex number which is similar to the polar form that corresponds to the length magnitude and phase angle of the sinusoid but uses the base of the natural logarithm e 2 718 281. Polar form of a complex number.

See more on vectors in 2 dimensions. The horizontal axis is the real axis and the vertical axis is the imaginary axis. We have met a similar concept to polar form before in polar coordinates part of the analytical geometry section. We sketch a vector with initial point 0 0 and terminal point p x y.

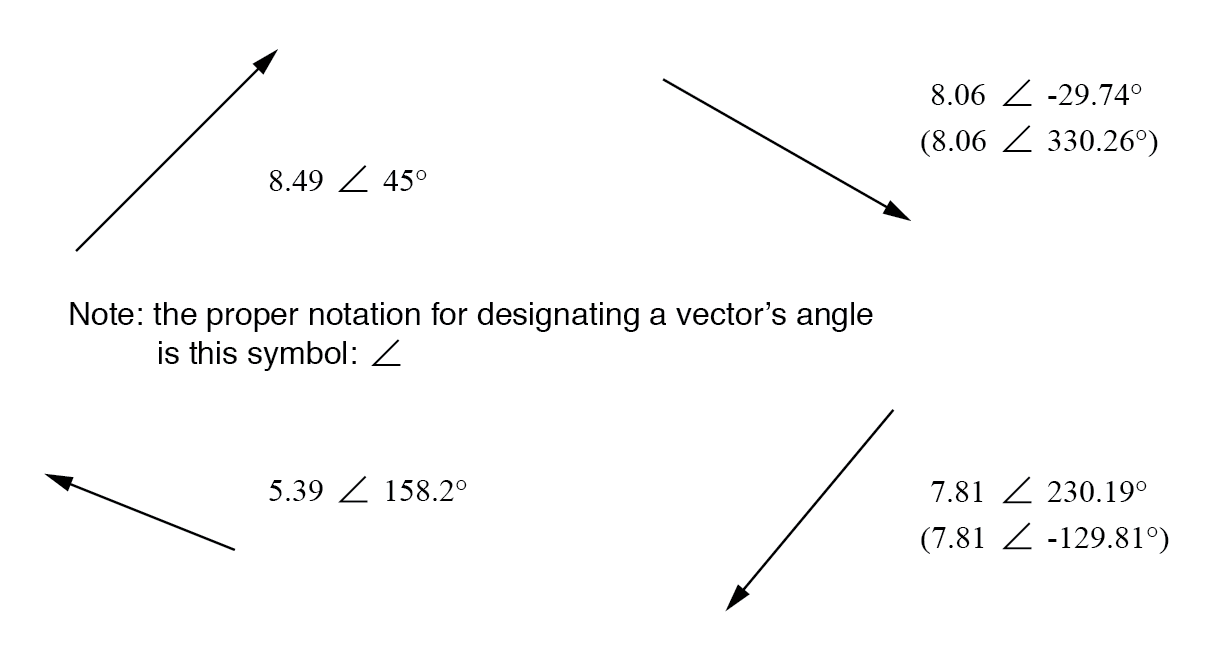
So far we have considered complex numbers in the rectangular form a jb and the polar form a θ. Now that we can convert complex numbers to polar form we will learn how to perform operations on complex numbers in polar form. We find the real and complex components in terms of r and θ where r is the length of the vector. Polar form of a complex number.

The polar form is where a complex number is denoted by the length otherwise known as the magnitude absolute value or modulus and the angle of its vector usually. This essentially makes the polar it makes it clearer how we get there in kind of a more i guess you could say polar mindset and that s why this form of the complex number writing it this way is called rectangular form while writing it this way is called polar form. For the rest of this section we will work with formulas developed by french mathematician abraham de moivre 1667 1754. The form z a b i is called the rectangular coordinate form of a complex number.

A complex number is a number that can be expressed in the form a bi where a and b are real numbers and i is a solution of the equation x 2 1 because no real number satisfies this equation i is called an imaginary number for the complex number a bi a is called the real part and b is called the imaginary part despite the historical nomenclature imaginary complex numbers are.